Cole Davidson

Sparse Image Processing

One of my favorite aspects of Computer Graphics is how large the field is. Topics like rendering, rasterization, and HCI are all very closely related to "classical" computer graphics, but more often than not, I have found it is quite simple to link Computer Graphics topics to my various courses in University. This project is no exception, these implementations of advanced image processing techniques were my final project for the course Sparse Matrix Computations.

Poisson Image Editing

Image compositing is the process of combining 2 pictures to create a new picture. Informally, image compositing can be thought of as "copying" a source image, S, and "pasting" it into target image T. In the naive image compositing algorithm, the pixel colors values from S are inserted into T directly. The results of this technique are shown below.

While fast and intuitive, this method has 2 limitations. It often produces visible seams between around the inserted region and the image lighting & coloring often mismatch. These shortcomings are largely due to the representations of images. A pixel is a collection of colors at a discrete location in a picture. Raw color data doesn't indicate an element's shape or features, such as whether a pixel is part of the dog's ear, fur, eyes, or tail. In Poisson image editing, Perez et al. developed Poisson image blending in an attempt to address these shortcomings.

Implementation

The main insight with drives Poisson image blending is that, given the gradient of an image and the pixel colors along the image boundary, all the original pixel colors can be recovered. This insight is a direct consequence of the finite differences equation. Using the finite differences equation to approximate the gradient between two pixels, p and q yields the equation:

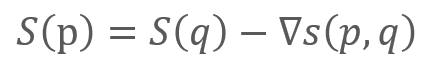
Instead of considering a pair of pixels, we can now consider how the gradient propagates color between all adjacent pixels. Let N_p represent the set of pixels adjacent to pixel p. Then combining the finite differences equations for all pixels in N_p yields the equation: Which, when rearranged, reveals the sparse system of linear equations to obtain the color for every pixel in an image:

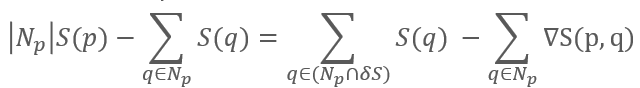
These equations are exactly the formulation for the discrete Poisson equation with Dirichlet boundary conditions, hence why the technique is called Poisson Image Editing. In reality, since the goal is to composite 2 images together, we take the boundary conditions from the target image, T, instead of using the boundaries from the source image. The results are shown below:

Mixed Image Blending

A notable limitation of seamless image blending is how the method handles images with holes. Colors are propagated through the empty regions and create prominent blobs. To address this deficit, Perez proposed a piecewise gradient operator expressed as: This gradient is a piecewise combination of the source image S and target image T gradients at each pixel in the reconstruction region. It preserves details in the target image by selecting the dominant gradient of both images. As a result, any mundane details, such as white spaces between letters, are discarded during image blending.

Image Colorization Using Optimization

While researching Poisson Image editing, I stumbled across a fascinating paper, Colorization Using Optimization by Levin et al. The methods proposed in this paper aimed to provide an artistically-friendly method for recoloring grayscale images. All an artist needs to do is scribble on each item in the picture, then the colors are propogated automatically throughout the image.

Implementation

The process of recoloring an image can be reframed as a data interpolation problem. Levin et al. make the observation that, in a grayscale image, neighboring pixels with similar brightness values often represent the same object, and thus should have the same color. Therefore, it is possible to utilize a weighted graph to propogate colors. For pixels p and q, the weight of edge {p,q} is given by:

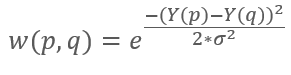
Propogating colors can be expressed as a quadratic optimization problem, which aims to minimize the difference in the colors of neighboring pixels:

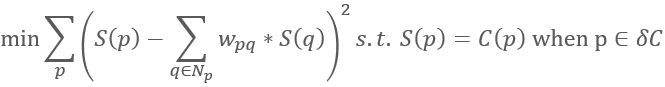
Where S is the recolored image, C is the artist defined colors, and δC is the set of all colored pixels in the original grayscale image. Quadratic Optimization Problems can be reformulated as a sparse linear system of equations. The solution to the linear system is a vector which encodes the new color at each pixel in the image. The results speak for themselves: